En 1952, David Huffman propuso un método estadístico que permitía asignar un código binario a los diversos símbolos a comprimir (píxeles o caracteres, por ejemplo). La longitud de cada código no es idéntica para todos los símbolos: se asignan códigos cortos a los símbolos utilizados con más frecuencia (los que aparecen más a menudo), mientras que los símbolos menos frecuentes reciben códigos binarios más largos. La expresión Código de Longitud Variable (VLC) se utiliza para indicar este tipo de código porque ningún código es el prefijo de otro. De este modo, la sucesión final de códigos con longitudes variables será en promedio más pequeña que la obtenida con códigos de longitudes constantes.
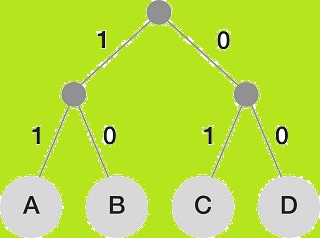
El codificador Huffman crea una estructura arbórea ordenada con todos los símbolos y la frecuencia con que aparecen. Las ramas se construyen en forma recursiva comenzando con los símbolos menos frecuentes.
La construcción del árbol se realiza ordenando en primer lugar los símbolos según la frecuencia de aparición. Los dos símbolos con menor frecuencia de aparición se eliminan sucesivamente de la lista y se conectan a un nodo cuyo peso es igual a la suma de la frecuencia de los dos símbolos. El símbolo con menor peso es asignado a la rama 1, el otro a la rama 0 y así sucesivamente, considerando cada nodo formado como un símbolo nuevo, hasta que se obtiene un nodo principal llamado raíz. El código de cada símbolo corresponde a la sucesión de códigos en el camino, comenzando desde este carácter hasta la raíz. De esta manera, cuanto más dentro del árbol esté el símbolo, más largo será el código.
Analicemos la siguiente oración: «COMMENT_CA_MARCHE». Las siguientes son las frecuencias de aparición de las letras:
| M | A | C | E | _ | H | O | N | T | R |
| 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |
Éste es el árbol correspondiente:
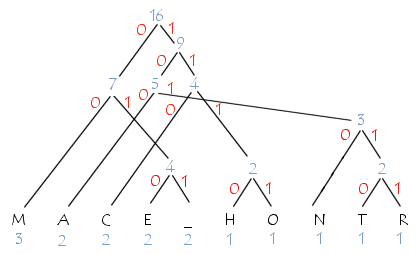
Los códigos correspondientes a cada carácter son tales que los códigos para los caracteres más frecuentes son cortos y los correspondientes a los símbolos menos frecuentes son largos:
| M | A | C | E | _ | H | O | N | T | R |
| 00 | 100 | 110 | 010 | 011 | 1110 | 1111 | 1010 | 10110 | 10111 |
Las compresiones basadas en este tipo de código producen buenas proporciones de compresión, en particular, para las imágenes monocromáticas (faxes, por ejemplo). Se utiliza especialmente en las recomendaciones T4 y T5 utilizadas en ITU-T