LA SUCESION DE FIBONACCI

Leonardo de Pisa, Leonardo Pisano o, más conocido como “Fibonacci”, su apodo, fue un matemático italiano del siglo XIII, hijo de un mercader viajante cuya educación fue dejada a cargo de unos moros en Argelia, quienes le transmitieron parte de su cultura.

Con una trayectoria muy prolífica en las Matemáticas y tan solo 27 años, escribió el “Liber Abaci”, su primera obra. Sin embargo, su fama superior se debe fundamentalmente a dos cosas:
La primera, es que introdujo en Europa el uso de los números arábigos y por lo tanto, también el cero. Facilitando así los cálculos y la contabilidad que, por esas épocas se realizaban en números romanos. Pero, a pesar de lo que hoy parecería obvio, se tardó nada menos que tres siglos en adoptar totalmente la numeración arábiga.
La segunda y más famosa contribución es la sucesión de números que lleva su nombre y que, en forma sorprendente, acerca las matemáticas a la naturaleza.
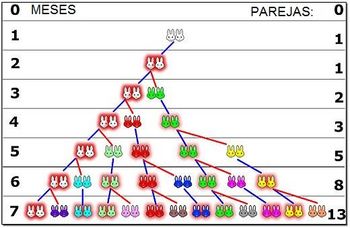
La “Sucesión de Fibonacci” nació de estudiar la procreación de los conejos y es así:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ….
Es una sucesión infinita donde cada término se obtiene sumando los dos anteriores y cuyos números también son conocidos como “números Fibonacci”
La sucesión de Fibonacci y sus números cumplen un montón de propiedades. Veamos algunas de ellas:
Cualquier número entero se puede expresar como una suma de números de Fibonacci.
Tan solo un término de cada tres es múltiplo de 2, uno de cada cuatro es múltiplo de tres y uno de cada cinco es múltiplo de cinco y así sucesivamente.
El máximo común divisor de dos números de Fibonacci cualquiera es otro número de Fibonacci.
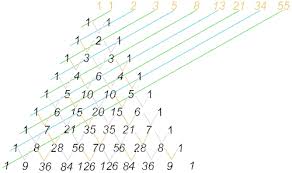
También aparecen en el Triángulo de Pascal
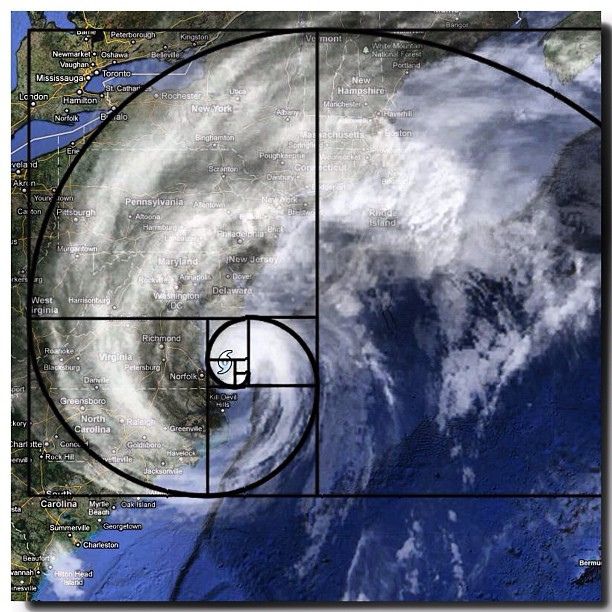
Pero lo que hizo más famosa a la sucesión de Fibonacci fue que aparece mucho en la naturaleza, en cómo se disponen las ramas de los árboles, en cómo se distribuyen las escamas en piñas, en como se van formando los pétalos de la alcachofa y de las flores, en la distribución de los granos del girasol, en los caparazones de los caracoles y hasta en la forma de las galaxias espiral y las tormentas.
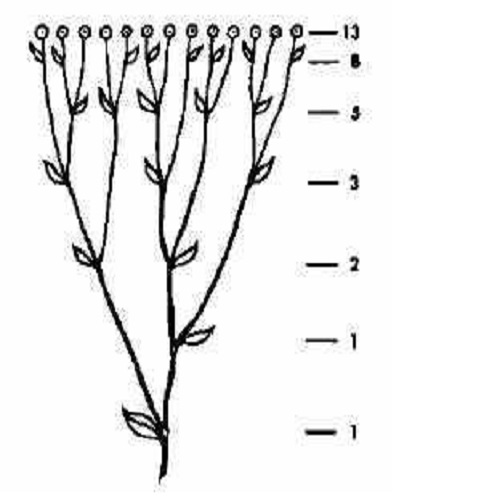
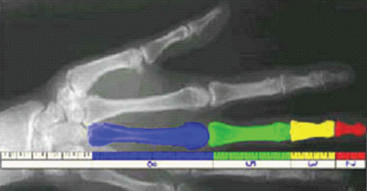
Pareciera que la naturaleza sigue un orden matemático, la sucesión de Fibonacci hasta puede encontrarse en el cuerpo humano, por ejemplo en la relacion de la longitud de los huesos de las manos.
También aparece en la arquitectura, en la música y en el arte. Así podemos encontrarla en las obras de Leonardo Da Vinci, en las partituras de Beethoven y en el Partenón.
Fibonacci está en algo tan esencial como son los acordes musicales. Un ciclo completo en un teclado de piano desde la nota Do hasta la siguiente nota Do (llamado “octava”), incluye trece notas, que es número de la sucesión de Fibonacci.
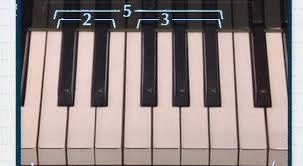
En un teclado, en cada octava, hay 8 teclas blancas y 5 negras, agrupadas en conjuntos de 2 y 3. Por supuesto, 2, 3, 5 y 8 son parte de Fibonacci.
Es más, si yo toco la nota Do, y al mismo tiempo, toco una nota separada dos teclas, y otra nota separada tres teclas, hago un acorde “mayor”. Y así, para definir la nota “tónica”, o sea, la que “predomina” en un acorde, también se recurre a números que siguen esta serie. Por lo tanto, mucha de la música que escuchamos, incluye esta increíblemente versátil y hermosa proporción.
Pero, todavía hay algo más que encierra la Sucesión de Fibonacci.
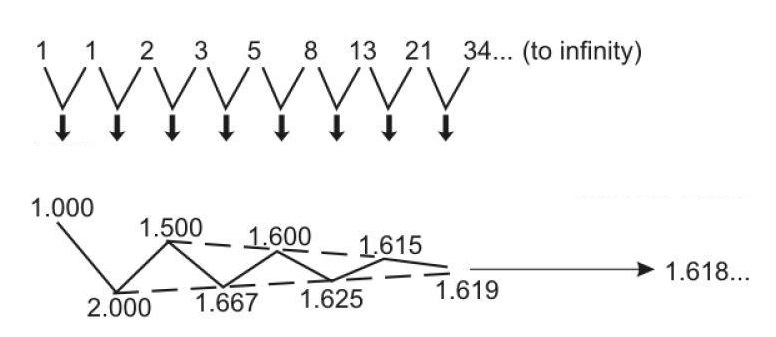
Si se toman dos números consecutivos de la Sucesión de Fibonacci, y se divide el mayor por el menor, conforme avanzamos en los términos de la sucesión, estos cocientes comienzan a acercarse al valor de la “relación aurea”, “número áureo”, o más conocido como Φ (Fi)
El primero en hacer un estudio formal del número áureo fue Euclides, un matemático y geómetra griego que vivió en Alejandría alrededor del año 250 ac.
Euclides definió la razón aurea con un segmento cualquiera de recta al que se lo divide en dos (a y b) tal que cumplieran la siguiente condición:
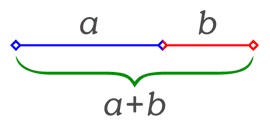
a/b = (a+b)/a
Es decir que el segmento menor es al segmento mayor, como este es a la totalidad.
Se establece, por lo tanto, una relación de tamaño entre los segmentos en que queda dividido el segmento original, esta proporción se llama la proporción dorada o la proporción aurea (de oro).
Si resolvemos esta ecuación para obtener el valor de Φ, considerando que Φ = a/b, nos queda:
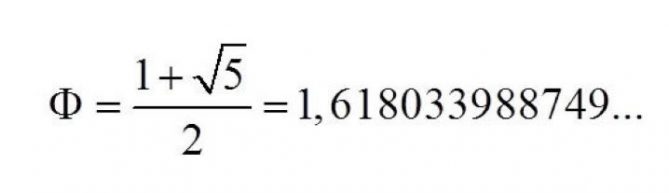
Podemos ver el desarrollo de la solución completa en la nota «Calculo del número Φ»
Si esta relación se lleva a los lados de un rectángulo, obtenemos un rectángulo áureo y este a su vez se puede construir usando cuadrados con la sucesión de Fibonacci. Finalmente, partiendo de estos cuadrados podemos construir la Espiral de Fibonacci (o aurea, o logarítmica) presente en los caracoles, la formacion de tormentas y las galaxias espiral, entre otras expresiones del universo.